Back to main page

Dimensionality Reduction

Curse of dimensinality

Why dimensionality reduction?

• Visualization
• Remove multicolinearity
• Remove redundant features
• Deal with the curse of dimensionality
• Identify structure for supervised learning
• High-dimensional data

Concept

• Dimensionality reduction is a process of reducing the number of random varialbes under consideration by obtaining a set of principle variables.
• Approaches can be divided into feature selection and feature extraction.

Types

• Feature subsetting
• Matrix decomposition
• Manifold learning

Common methods of dimensionality reduction

1. Principal component analysis (PCA)
   • Linear dimensionality reduction
   • Extract “principal components” that are uncorrelated with each other to represent the variance in the data
   • Generate ranked list of “principal components” that explain high to low fraction of variance
   • Typically works in Euclidean space (linear), not suitable for data on a non-euclidean space (non-linear) or contain fine structures
2. Kernel PCA
   • Employ kernel trick to PCA to increase capacity of nonlinear mapping
3. Linear Disriminant Analysis (LDA)
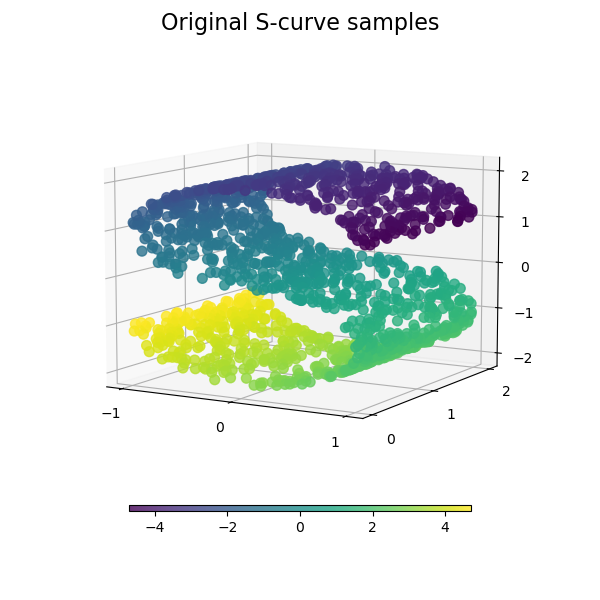
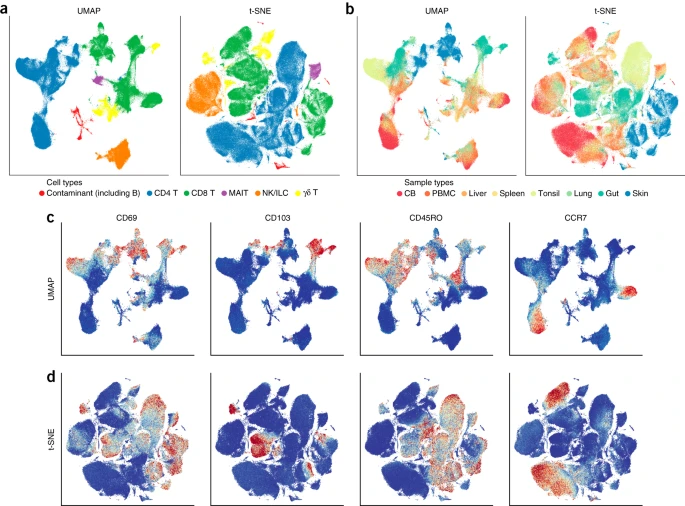
4. T-distributed Stochastic Neighboring Embedding (t-SNE)
   • Non-linear dimensionality reduction
   • Model each high-dimensional object by a 2 / 3 dimensional point in way that similar objects are modeled by nearby points and dissimilar objectes are modeled by distant points
   • Based on neighboring map
   • Developed from Stochastic Neighbor Embedding (SNE)
5. Uniform Manifold Approximation and Projection (UMAP)
   • Non-linear dimensionality reduction
   • Based on neighboring map & topological data analysis method

Benchmarks

• Scikit-learn Manifold Learning
• t-SNE v.s. PCA handwritten digits
• Becht, Etienne, et al. “Dimensionality reduction for visualizing single-cell data using UMAP.” Nature biotechnology 37.1 (2019): 38.

Reference

1. Dimensionality reduction algorithms: strengths and weaknesses
2. Gunasekaran, Mr Ramkumar, and Mr Tamilarasan Kasirajan. “Principal Component Analysis (PCA) for Beginners.” (1901).
3. Hinton, Geoffrey E., and Sam T. Roweis. “Stochastic neighbor embedding.” Advances in neural information processing systems. 2003.
4. Maaten, Laurens van der, and Geoffrey Hinton. “Visualizing data using t-SNE.” Journal of machine learning research 9.Nov (2008): 2579-2605.
5. McInnes, Leland, John Healy, and James Melville. “Umap: Uniform manifold approximation and projection for dimension reduction.” arXiv preprint arXiv:1802.03426 (2018).
6. I Goodfellow, Y Bengio, and A Courville. Deep Learning. MIT Press, 2016